Two-Step Algorithm

This section describes the two-step algorithm for survival analysis using the cenreg package. The two-step algorithm is a method for estimating survival functions in the presence of censored data.

First Step: Censored Joint Distribution Estimation

Let \((x,t,e)\) be a data point for survival analysis, where \(x\) is a feature vector, \(t\) is the time of the event or censoring, and \(e\) is an event indicator (1 if the event occurred, 0 if censored). If the time horizon is descretized, each \((t,e)\) can be represented as a vertical line segment (if \(e=0\)) or a horizontal line segment ( (if \(e=1\))) in the two-dimensional space as shown in this figure.

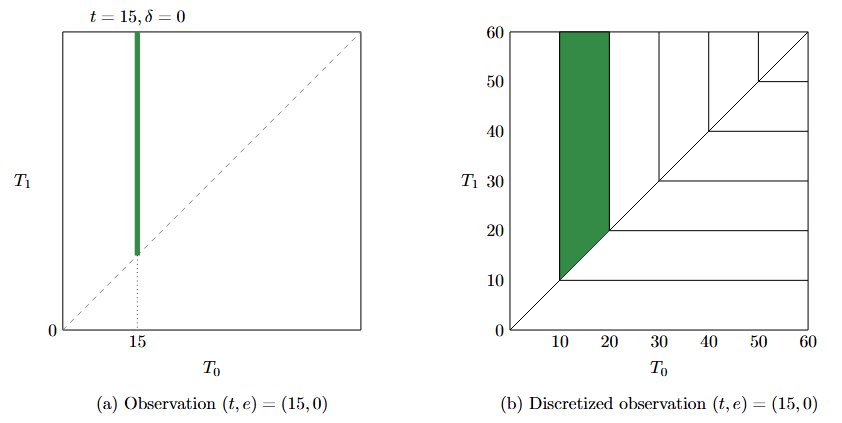
_images/cjd_discretization_0.png — Censored Joint Distribution

The first step of this algorithm estimates the distribution of the discretized observations by using a density model (e.g., LightGBM, neural network, etc.).

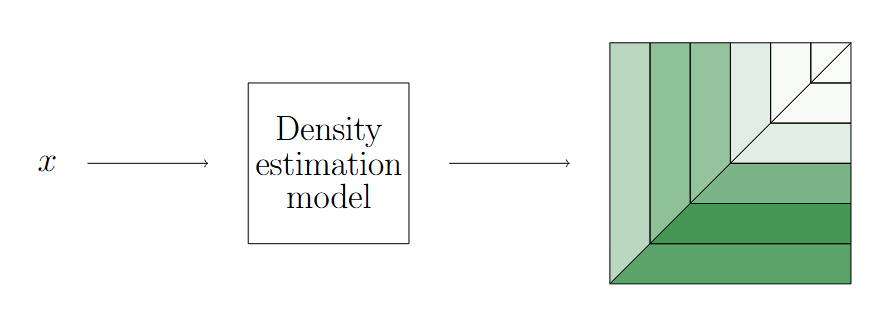
_images/density_estimation.png — Density Estimation

Second Step: Estimate Survival Functions

The second step of this algorithm compute the survival function (equivalently, the CDFs of \(T_0\) and \(T_1\)) from the estimated distribution.

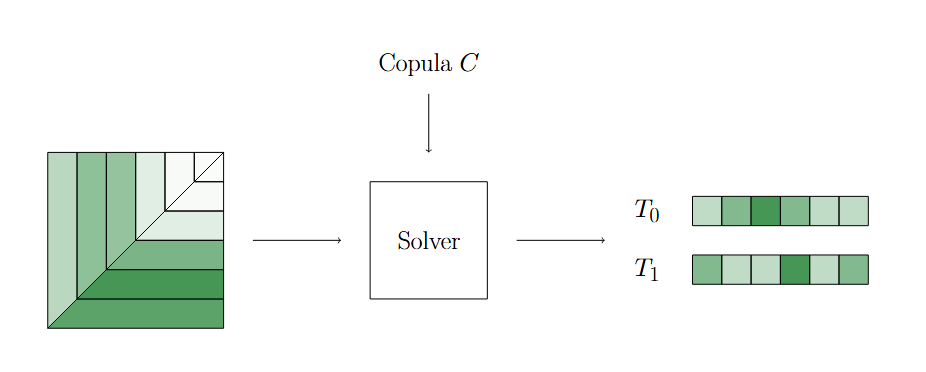
_images/solve_eq_with_copula.png — Estimate Survival Functions

Jupyter Notebooks

We provide Jupyter notebooks that demonstrate the two-step algorithm using different models. You can find these notebooks in the notebooks directory of the cenreg repository.

TS-LGB: An implementation with LightGBM
TS-Brier: An implementation with a neural network whose loss function is the Brier score